The incredible quantum computer simply explained

Quantum computers use the enigmatic quantum mechanics to provide completely new types of computing systems . That’s why quantum computer properties have an almost incredible effect: For example, the performance of a quantum computer increases ” exponentially”, so to speak explosive, with increasing size. In the following I will explain the special properties of a quantum computer in simple words and I will go into more detail about the amazing quantum programs .

The bang: the Shor algorithm

In 1994, mathematician Peter Shor from the renowned Massachusetts Institute of Technology / MIT had the idea of ​​his life. An idea that would herald a new era.

Shor investigated a new method to break down an integer into prime numbers. This prime factorization is an extremely complex matter. Even very powerful supercomputers take several years to break down very large numbers into prime numbers. ⁱ

This is one of the reasons why it is used for secure data encryption on the Internet. It is very easy to assemble even large numbers from known prime numbers (e.g. 7 × 13 × 13 × 17 × 53 = 1065883). Since the reverse is almost impossible, encryption on the Internet is bombproof.

Actually!

Shor wondered if the new method could be used to create new prime number algorithms. At some point he remembered a compulsory lecture on quantum mechanics, which he had had to listen to when he was a math student at the California Institute of Technology (Caltech). He had the terrific idea that the method could achieve the goal much faster if the calculation was not a conventional computer, but a quantum computer. He spent a year tinkering with his quantum algorithm and in the end actually came to the desired result ⁱⁱ.

Shor’s algorithm hit like a bomb. Up to this point, no one had been able to build a quantum computer. However, the Shor algorithm was the first proof of how immensely powerful a quantum computer would be and what social effects it would have. Shor’s algorithm triggered a veritable boom in the quantum computer scene.

A quantum computer takes advantage of the extraordinary properties of the atomic world to achieve completely new dimensions in computing speed using special quantum programs, the quantum algorithms. The word “extraordinary” is probably still understated . The quantum world is a puzzling world with almost magical properties.

To get an idea of ​​what is special about a quantum computer, we first have to look at how a conventional computer works.

Simply Explained: How does a conventional computer work?

Let us take the computer you are reading these lines with. It controls information in the form of zeros and ones via bits or bytes. The number “71” is represented, for example, by the bit series “0100 0111” and the letter “J”, by convention, by the bit series “100 1010”. Your computer remembers whether a row of bits represents a number, a letter, an image, or music. The bits themselves exist in the form of billions of electrical on / off switches, the transistors. Together they form the main memory of your computer. A good conventional computer has about 16 * 8 billion bits, or in other words: 16 gigabytes. A computer program manipulates these bits in individual arithmetic steps using the most elementary building blocks of human logic: AND operations, OR operations, NOT operations. These links are also called “gates” (English gates). A NOT link reverses a single bit, for example, to its opposite: NOT 0 = 1, NOT 1 = 0.

Using clever electrical circuits, the data bus, your computer is able to selectively control, read or overwrite each of the countless bits in the working memory with new values. A calculation step then looks like this, for example:

“Read out the value of the bit with the address number 1543216 and the value of the bit with the address number 6543 and combine the two values ​​with an AND command. Save the result in the bit with the address number 789874 “. By cleverly arranging these elementary AND, OR, NOT connections, one after the other, your computer can, for example, take two numbers together. After each of these calculation steps, your computer writes the intermediate results back into the main memory and calls them from there again for the next calculation step. The program for taking pictures looks unnecessarily complicated and mechanically stupid. However, since your computer is capable of executing billions of arithmetic steps per second, it is ultimately superior to every human being in such tasks.

The qubits simply explained

In contrast, a quantum computer does not control the information via simple on / off switches, i.e. the conventional bits, but via so-called “qubits” (for quantum bits). In a qubit, the values ​​0/1 or on / off are simultaneously available in a superimposed form. At first glance, this may look harmless. In fact, this overlay is one of the great mysteries of quantum mechanics.

As a consequence, the Austrian Nobel Prize winner Erwin Schrödinger invented his famous thought experiment “Schrödinger’s Cat” almost a hundred years ago: a cat that is overlaid with a qubit. The qubit turns on a poison cocktail as soon as it has the value 1. If the qubit has the value 0 and the value 1 at the same time, according to Schrödinger, the cat should also be dead and alive at the same time.

In my article “The Qubit and a Magician at Britain Has Got Talent” I compare the Qubit with a spectacular magic trick by the magician Darcy Oake in the 2014 English talent show. Darcy Oake appears to be on stage twice at the same time. A qubit behaves the same way. Not as a trick, however, but in reality.

To illustrate this, I use a qubit representation on “quantum-computer-explained.com”, which is simplified compared to the textbook representation but is very close to the core: a simple pointer in one level. For example, the following qubit is in equal parts both in state 0 and in state 1.

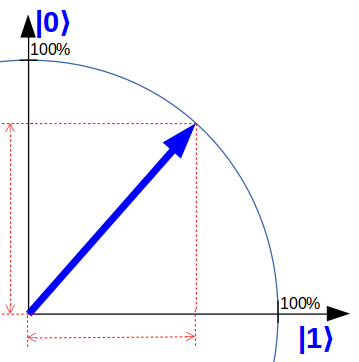
If you think now: “Got it! Then two qubits would simply be two pointers, ”I unfortunately have to disappoint you. The quantum computers don’t make it that easy for us. In fact, two qubits in the simplified representation still correspond to one pointer , but with four vertical axes !

I know that any attempt to somehow visualize four dimensions ends miserably. I want to try anyway:

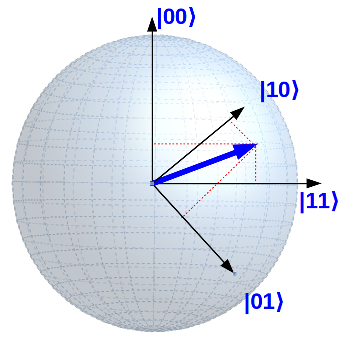
You can imagine that this behavior has very unusual consequences … More on this in the section on “Quantum Entanglement”.

The second such extraordinary feature of qubits is the following. Even the smallest amount of qubits in a quantum computer can simultaneously absorb and process a huge amount of information: ⁱⁱⁱ

• • • 1 qubit corresponds to 2 conventional bits
    • 2 qubits correspond to 4 conventional bits
    • 10 qubits correspond to 16 conventional kilo-bytes
    • 20 qubits correspond to 16 conventional megabytes
    • 30 qubits correspond to 16 conventional gigabytes
    • 31 qubits correspond to 32 conventional gigabytes

Each additional qubit doubles the number of information that can be used simultaneously! The performance of a quantum computer increases exponentially ! And this is how it goes on:

• • • 45 qubits correspond approximately to the memory size of the largest current, conventional supercomputer

• • • 50 qubits, the “quantum superiority” limit: The, at least theoretical, limit at which a quantum computer can perform certain calculations that would not be possible with any of the current supercomputers. ^iv The tech giants are battling it out at exactly this limit.
  • • 250 qubits: the absolute limit that would even be feasible for conventional computers. To achieve the memory size of a 250 qubit quantum computer, a conventional computer would have to use every atom in the universe as a conventional bit.

It sounds incredible. And it is!

And now consider that the quantum computer industry has the goal to build quantum computers with millions of qubits!

Quantum computers simply explained: quantum parallelism, superposition

The punch line with these enormous numbers is actually the following: let’s take the example with the take again. Your conventional computer takes two numbers , in the form of two rows of bits in the working memory, executes the specified program of individual arithmetic steps and finally receives one number in the form of a row of bits.

In contrast, a quantum computer takes two qubit rows for a task, saves the intermediate results again in qubits and finally receives the result in the form of a qubit row ^v. However, since a qubit series can contain huge amounts of information at the same time (see above), the quantum computer can ultimately execute the program simultaneously with a huge amount of numbers. This is the quantum parallelism. Usually, however, one speaks of “superposition”.

In fact, this form of overlay occurs more often in nature and not only in quantum mechanics ^vi. What makes quantum parallelism so special is the fact that only a few qubits can overlay such unimaginably large amounts of data. The qubits are not only superimposed individually, but the entire network of qubits. And it is precisely here that the number of possible combinations increases so rapidly. For three qubits, for example, up to eight possible bit states are used simultaneously (this corresponds to 2 ³ ): namely 000, 100, 001, 101, 011, 111, 010 and 110.

But: Every measurement destroys the quantum properties

Unfortunately, the enormous parallel computing power of a quantum computer has a big catch: it only works as long as the quantum computer is perfectly isolated from its surroundings and the highly fragile qubits are undisturbed. By reading the result of the quantum program from the qubits at the end, however, we are doing exactly that. At this moment, the values ​​that are present “decay” and only a single value remains, which is also chosen at random . This decay is known as the “collapse of the wave function” and is yet another mystery of the quantum world. It was the reason why some physicists, including Albert Einstein himself, appreciated and pushed quantum theory but basically rejected it: “God does not throw dice”.

Incidentally, such disturbances have almost insoluble consequences for the construction of quantum computers. How you can “protect” quantum properties against it, and what fundamental meaning this “quantum error correction” could have even for the nature of space and time, I will explain in the next Artikel „Der sehr, sehr steile Weg zum ersten Quantencomputer“.

And now? What is won if everything ultimately depends on pure chance?

Now comes the but: We can influence the probabilities with which the various values ​​are ultimately read out or measured. The art of a quantum program is, among other things, to manipulate the qubits in such a way that the result sought is most likely to be measured in the end. Until then, i.e. while he is still isolated from his surroundings, the enormous computing power of the undisturbed quantum computer can be used.

You can find out more about quantum programs below. Let us first come to one of the strangest properties of quanta or qubits.

Einstein’s spooky entanglement

I had already shown a pointer example for two qubits above. This pointer property has a bizarre consequence. In 1935, Albert Einstein personally predicted it in a famous essay: The “quantum entanglement” (English “entanglement”, he himself referred to the phenomenon as “spooky long-distance effect”). We can overlay two qubits (or several qubits) in such a way that we can no longer recognize them as individual qubits. Instead, they form a completely new, uniform state. They appear “entangled”: A measurement on the first qubit has an immediate effect on the second qubit.

To clarify this, let’s look again at a pointer diagram with 4 axes. The blue pointer below describes the common state of Qubit A and Qubit B. Now we only measure on Qubit B. In the previous section, you learned that qubit B decides on a state by measuring : We measure either state 0 or state 1 . We have not yet carried out a measurement on Qubit A. In fact, for Qubit A , we should have received a single, superimposed pointer in two dimensions that “knows ” nothing about the previous and independent measurement on Qubit B.

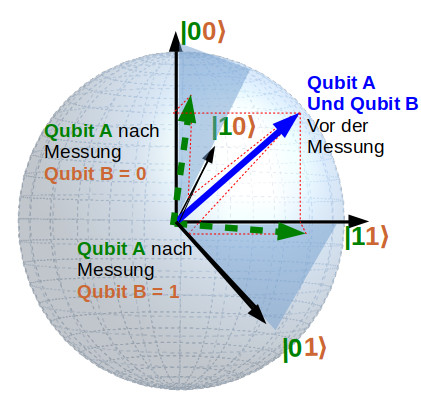
You can see from the example, however, that the measurement has a direct effect on Qubit A. After the measurement, Qubit A is something like the “shadow” of the original blue pointer , which I indicate with the dashed pointer. The level in which this shadow lies is determined by the measurement of Qubit B : If we measure the state 0 for Qubit B , we get for Qubit A the left dashed pointer, which mainly points in the 0 direction . If we have the state 1 for Qubit B, we get the lower dashed pointer for qubit A, which mainly points in the 1 direction .

The goal of Einstein’s work was actually to prove a fundamental mistake in quantum mechanics . According to Einstein, this entangled entity would have to remain, even if the two qubits were light years apart . That is why he spoke of long-range effects . The crazy thing is: all experiments suggest that it is the same. The long-distance effect is real in the quantum world and it has an immediate effect !

Such entangled forms of state do not exist anywhere else in the natural sciences . Maybe with one exception: a so-called astronomical “wormhole”, which can connect two black holes over a distance of many light years, as a kind of hyper-expressway. The question of how these two phenomena are related is actually the subject of current research in theoretical physics.

Quantum gates simply explained: The building blocks of quantum programs

We can’t just run the same algorithms that work on a conventional computer on a quantum computer. Instead, we have to construct completely new and strange quantum algorithms for quantum computers.

For this purpose, a quantum computer also uses elementary logic modules, the “quantum gates” (quantum gates) in every calculation step. However, these do not reflect our normal everyday logic, but rather quantum logic: The elementary building blocks are therefore no longer called AND, OR or NOT. Instead, a quantum computer uses logic modules that are called Hadamard, X, S, T, Z, Controlled NOT or Controlled Z, for example. The way these quantum gates function is less like the known building blocks of our everyday logic than they are rotations in a huge abstract “hyperspace” (or more precisely: a “Hilbert” space). In their entirety, the qubits form a single pointer in this space, which is rotated by each individual quantum gate. For two qubits, you had an impression of it earlier.

This fundamental strangeness compared to our everyday logic is the reason why a quantum program can only be deciphered and understood by connoisseurs of quantum algorithms.

For all representations of quantum gate circuits I use the excellent quantum computer simulator “Quirk” on “quantencomputer-info.de”:

http://algassert.com/quirk

Quirk is publicly available and can be tried directly in your browser (via “WebGL”). Craig Gidney, the Quirk programmer, modeled a number of well-known quantum algorithms. You should definitely take a look there. My favorite is the “quantum teleportation”, in which the author uses an animation to very nicely illustrate how a qubit state can be tele-transported to a second qubit by entangling it over a distance. By the way, Gidney is now employed by Google and has developed the quantum programming interface “Cirq” in the lead.

In every area of ​​conventional programming there is a lively IT scene on the Internet that has a strong influence on further development: be it servers, networks. Databases, Internet, programming, … The IT scene for quantum programming is still mainly located in the research facilities of universities and mainly in the special departments of Google, IBM, Microsoft & Co and some startups for quantum computers. Since spring 2018 there has been the new discussion forum “Quantum Computing Stack Exchange” ^vii , which is developing very lively and with high quality content. Important results will still be published on complicated scientific papers.

The most significant consequence of this publication was Peter Shor’s algorithm from 1994, which is able to crack the data encryption that was believed to be secure on the Internet. In the meantime, other, extremely fast and probably also more interesting quantum algorithms have been constructed.

Example from the Quirk homepage: Schematic structure of the Shor algorithm.

All providers of quantum computers have now developed programming interfaces. Via these interfaces, the quantum programs can be executed either by simulator on your own PC or from your own PC by remote control on the manufacturer’s cloud quantum computer. The following program excerpt shows Google’s example of the Shor algorithm in Google’s own programming interface “Cirq”.

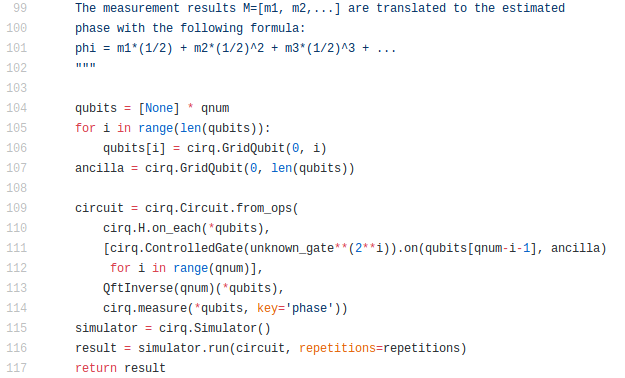
You can also see from these examples how much quantum programming is still in its infancy. All programs are currently still written in a kind of “machine code for quantum computers” and are therefore difficult to decipher. In the coming years and decades, quantum programming will also have to develop further in this regard. The software development for conventional digital computers showed us how. In the course of time, more and more intuitive programming languages ​​have emerged that abstract the actual machine code better and better.

Find the Ace of Spades! A quantum algorithm simply explained

To give you an impression of the different nature of the quantum algorithms, let’s try to solve the following problem:

Someone shuffles a card game with 52 cards well for us and spreads out the 52 cards indiscriminately and face down in front of us. Now he writes a number on each back of the card, the “address”. The task should be: Find the card, i.e. the address number, with the ace of spades!

With our everyday logic and for every conventional computer, the best algorithm for the solution is very simple and obvious:

• • • Step 1: take any card
    • Step 2: turn it over and check: is it the ace of spades?

• • • • • If so : You are done!
        • If not : You put the card aside and start again at step 1.

On average we need ½ * 52 = 26 runs for the solution. No single person and no single processor core could ever perform this task faster. Point!

The processor of a quantum computer can do this very well. For him, the solution looks completely different and bizarre. Because of the quantum parallelism, the quantum computer can view all cards at the same time and check them. He can, however, not easily fetch the card he is looking for, or more precisely the address number for this card. Instead, he has to gradually “hide” the wrong cards and gradually “show in” the ace of spades. In the end, only the ace of spades with the address number you are looking for remains.

The algorithm for this is the famous Grover algorithm. I introduce it in detail in my Artikel „Der Grover-Algorithmus und die Suche nach dem Heiligen Gral“You will also see how extremely important and profound this at first glance is banal question. The task could also be slightly modified: “Find the shortest route of all possible routes” or even “Find the proof for … (an important mathematical problem)”.

For our map example, the Grover algorithm works as follows:

In our quantum computer, we first assigned a bit pattern to each card. Ultimately, we are looking for the bit pattern for the ace of spades. Someone else has now “hidden” these bit patterns in the qubit registers of our quantum computer. We do not know where and instead we only get some address numbers for the respective registers. Of course, these address numbers are qubits again.

• • Step 1: First we convert the qubits of all address numbers into a uniformly superimposed quantum state.

• • Step 2: Then we reload the unknown bit patterns of the cards and “pin” them to their respective address numbers (this operation is also called “Quantum RAM”).

• • • • We now have a single state in which all cards including their address numbers are equally involved (the qubits of the addresses and the qubits of the bit patterns are maximally interwoven with each other).

• • • • You can “imagine” this state as a single pointer in a huge, abstract room with 52 dimensions or directional axes. But don’t try it at all. We can’t imagine more than three dimensions anyway: top / bottom, left / right, front / back.

• • • • Each of the 52 direction axes corresponds to a specific map. The Ace of Spades is one of these axes. Our superimposed state points completely obliquely into this room and a little in each of the 52 directions.

• • Step 3: The quantum computer now checks in which direction the ace of spades lies.

• • • • In principle, this test is a simple subroutine, it is nevertheless called something mysterious: the “oracle”. Figuratively speaking , the quantum computer uses the oracle to turn the pointer in the Ace of Spades direction.

• • • • Unfortunately, he can only turn it by a small angle. The more cards that need to be checked, the smaller this angle.

• • • • After the test, the pointer is no longer a uniform overlay. It now points a little more in the Ace of Spades direction than the directions of the other cards.

• • Step 4: We now have to perform step 3 several times in succession. The scientist Lov Grover demonstrated in 1996 that the pointer was turned in the direction of the ace of spades after √ 52 ≈ 7.2 tests . After 7 tests we measure the qubits and get the bit representation of the ace of spades and their address number.

The following example shows the Grover algorithm for two qubits.

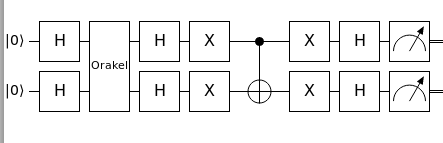
Quantum complexity simply explained

Half a century ago, computer scientists began dividing problems into classes depending on how difficult it was to find a solution. The problems that can be solved relatively effectively with a conventional computer are called P problems .

When the first concepts for quantum computers were developed, the problem class BQP was added. These are the problems that can be solved relatively effectively with a quantum computer.

It is now known that there is a fundamental difference between these two classes. In principle, a quantum computer is able to effectively solve much more problems than a conventional computer. An example of this is the division into prime numbers using the Shor algorithm.

The following diagram shows that even a quantum computer has its limits. It shows the relationship between the important problem classes that most computer scientists currently suspect (you can find out more about the classes shown in my article on the Grover algorithm):

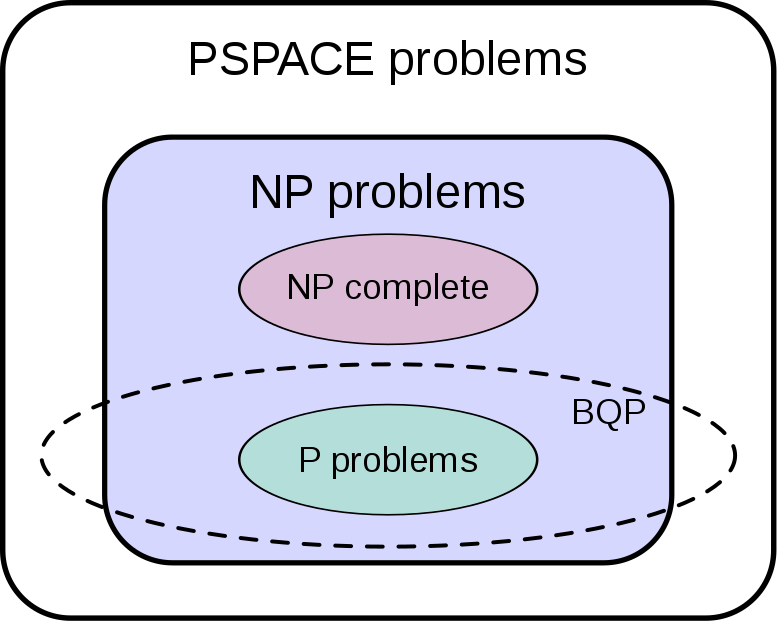
(Source: https://en.wikipedia.org/wiki/File:BQP_complexity_class_diagram.svg)

Footnotes