Google and the proof of quantum supremacy

Google has recently demonstrated the so-called “quantum supremacy”. Quantum supremacy is the major milestone in the development of current quantum computers. Quantum supremacy marks the point in computer history at which a quantum computer has been proven to outperform all conventional supercomputers for a specific problem for the first time. I explain all the details, the exciting backgrounds and give you detailed explanations of this probably groundbreaking event.

A magic moment of science and technology

Science usually means struggling for knowledge in painstaking detail work, putting away failures, rethinking and moving on. Science also means celebrating small successes every now and then, together with a small crowd of like-minded colleagues. Successes that have brought the big picture a yet another little bit forward, usually unnoticed by the masses.

And then there are the very rare, the really big moments: the magic moments of science and technology. The last major building block in a long chain of previous events that is so powerful that it forces an entire new branch of knowledge into the public eye.

The Internet company Google recently managed to make a bang:

The tech giant’s “AI Quantum” team recently demonstrated “quantum supremacy” .

Google’s proof of quantum supremacy: A rumor is confirmed

The first tangible signs of this were already published in June. The online magazine Quantamagazine reported on an ominous calculation for which the tech giant’s enormous computing resources had to be tapped. In July, the Forschungszentrum Jülich in Germany issued a press release on a new partnership with Google ⁱ. Later it turned out that the Jülich supercomputer also played a certain role in Google‘s results.

At the end of September, NASA, one of Google’s partners in the matter, made a confidential preliminary version of Google’s research work available for download. Yet this was probably for internal purposes only, for a short time and in a well-hidden area on the website. However, not hidden enough for Google’s own search engine: The automated Google “crawler” became aware of the document shortly after publication and distributed it by hand.

The news spread quickly and several news sites reported about it.

Finally, Google reacted and made the document called “Quantum Supremacy Using a Programmable Superconducting Processor” available for download themself (together with an additional article) ⁱⁱ. For the time being, however, completely uncommented, as the work was in the “peer review” stage at this point.

I emphasize that Google did not announce its groundbreaking results prematurely, but waited for the proper scientific review process.

Yesterday, the official publication was published in the journal “Nature” ⁱⁱⁱ.

At the center of the work is the previously unknown quantum computer “Sycamore” from Google and a calculation that would probably take 10,000 years on the currently fastest supercomputers: Sycamore only needed 200 seconds.

At the beginning of this week, the IBM group for quantum computers put some more spice into the current developments with an additional interesting detail: With its improved simulation process, the fastest supercomputer would probably only have taken 2½ days.

In the following you will find all the details and the exciting background to this, probably nevertheless, groundbreaking event.

The development of the first quantum computer

Deep down, nature does not function according to our everyday laws, but according to the mysterious laws of the quantum world. For this reason, conventional computers quickly reach their limits when it comes to calculating natural processes on an atomic scale. Over 30 years ago, the legendary physicist Richard Feynman left the world of science with a visionary but almost hopeless legacy: only if we were able to construct computers based on this quantum logic, we could ultimately simulate and fundamentally calculate nature.

Once this idea was born, the topic quickly took off. The first huge bang came in 1994 when mathematician Peter Shor demonstrated that the encryption on the Internet, which has been believed to be bomb-proof, could be cracked in a matter of seconds with a very large quantum computer (not that a false impression arises: Shor’s algorithm plays no role in Google’s proof of quantum supremacy).

Yet, the technical hurdles for the actual development were and still are enormous. It took almost 20 years before the first very experimental minimal quantum computer was built in a research facility.

The NISQ era of quantum computers

Over time, the tech giants IBM, Google, Microsoft and Co recognized the huge potential of the new technology. They started collaborations with research groups, recruited top-class scientists and got involved in the development of quantum computers.

As a result, the first quantum computers, offered by tech companies, are now available in the cloud. Available to everyone. I describe the current status in my article “Which quantum computers already exist?”

Current quantum computers still have a very small size of up to 20 “qubits”, the quantum bits. Just like conventional bits, qubits can be in the states 0 or 1. In addition, they can also be in “superposed” states of both 0 and 1.

To illustrate this, for “quantum-computer-explained” I use a qubit representation, which is simplified compared to the textbook representation, but gets already quite close to the core: A simple pointer in a flat plain. For example, the following qubit is in equal parts both in the state 0 and in the state 1.

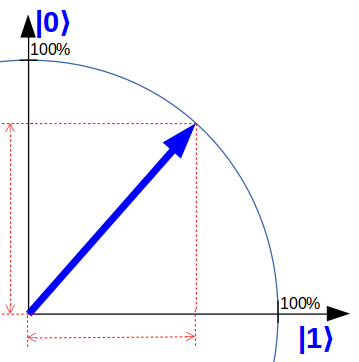During a quantum calculation, the qubits get “rotated” in the plain and are measured at the end. By this measurement, the qubits “choose” a single state to end up at: 0 or 1. This decision is made purely by chance and is subject to the laws of quantum mechanics. The more the qubit pointed in the direction of a state before the measurement, the more likely this state is being measured afterwards.

The real highlight is the following: A quantum computer doubles its potential computing power with each additional qubit: That is, exponentially!

You will find more about the fundamental differences between a conventional computer and a quantum computer in my introductory article “The incredible quantum computer simply explained” .

The current quantum computers are still in the so-called “NISQ era”. This stands for “Noisy Intermediate Scale Quantum”, i.e. error-prone quantum computers with a “moderate” size of a few hundred “qubits”, in perspective.

What is quantum supremacy?

To give you an impression of it: The Shor algorithm would probably require hundreds of thousands of qubits and millions of arithmetic operations.

The quantum computer community is therefore driven by a big question:

Can you already do a calculation on a quantum computer,

1. 1. 1. that has a real practical use and
      2. that no conventional supercomputer could ever do?

Over the years, several practical quantum algorithms have actually been developed that can even run on current quantum computers. The problem is, that these calculations could be carried out easily even with a normal laptop.

By now it has become obvious that the search for such an algorithm is currently a too great task.

For this reason, the community has focused on point no. 2 for the past years: Is a current quantum computer able to outperform even the largest supercomputer for a single calculation, regardless of whether it has any practical use or not?

And this is exactly what quantum supremacy is all about.

John Preskill from the California Institute of Technology (Caltech), one of the leading scientists in quantum computer research, had calculated the sound barrier of quantum supremacy in 2012 ^iv. By this he has also given the go-ahead for a technological race. With a size of 49 or 50 qubits, a quantum computer should be able to perform certain calculations much faster than any conventional supercomputer. A quantum computer with this size should be able to show off its inherent and deeply built in speed advantage.

What is the significance of Google’s proof of quantum supremacy?

So to prove quantum supremacy, you only need a single calculation.

On the one hand, this claim sounds a bit ridiculous. As to say “Let‘s make it as simple as possible so we will succeed for sure”. Real “supremacy” should look different: For every other computing task, conventional computers are still miles ahead of current quantum computers.

On the other hand, the project also sounds absolutely absurd: Even a normal laptop works with billions of conventional bits and several processor cores. A supercomputer in turn operates in spheres that are several orders of magnitude higher. For many decades, computer science and IT have been working to make computer programs even better, faster. We can admire the success of these developments all around us in our digitized world.

It is therefore completely absurd to assume that we could construct any new type of programmable, universal computing machine, with just a few dozen “whatever bits” that could compute just a single task fundamentally better than the very best of our celebrated computers.

Ultimately, this is just what an “ancient” hypothesis from the early days of theoretical computer science deals with: The “Extended Church Turing Thesis”. It says just the opposite: Any type of universal computing machine can be efficiently mimicked or simulated by a conventional computer, and the opposite direction is just as true ^v. Or to put it more simply: We can continue to improve our computing techniques and the technology in our computers, but we can not fundamentally improve the very nature of our computing machines.

Anyone who demonstrates quantum supremacy has disproved the famous extended Church Turing thesis!

This is a fact.

Let‘s also get back to this „great moment“-thing: The miracle of such moments was often enough the prove of what is generally feasible.

Take the Wright brothers’ maiden flight, for example: On December 17, 1903, Orville Wright flew the first flight of a navigable propeller machine: 12 seconds long and 37 meters far. Thus, very manageable and actually not worth mentioning. Nevertheless, this moment has entered the history books ^vi. By the end of 1905 the brothers had been flying for almost 40 minutes and 40 kilometers.

We have to wait and see how the quantum computers will do …

Google’s way of proving the quantum supremacy

To demonstrate quantum supremacy, Google’s team had to master five extremely difficult tasks:

1. 1. 1. They had to design a universal quantum computer with about 50 qubits that was reliably able to correctly execute any quantum program.
      2. They had to find a calculation that was specially designed for this quantum computer and that actually uses all of its qubits and all standard operations for quantum computers (any other task could probably be efficiently accomplished by conventional computers).
      3. They had to do this calculation on the quantum computer.
      4. They had to demonstrate that the final result of the calculation is most likely correct.
      5. They had to demonstrate that no conventional computer can perform this computing task in a timely manner, not even the fastest supercomputers.

Of all these tasks, the first task was certainly the most difficult one.

Google’s team forms

Google has gained experience in the field of quantum computers for several years and in 2013 founded the “AI Quantum” team, led by the German IT specialist and long-time Google employee Hartmut Neven. Previously, Neven was a leader in the Google Glass project.

In 2014, Neven’s team started a collaboration with the well-known physicist John Martinis from the University of California, Santa Barbara. He was to lead the construction of a new quantum computer. Martinis team is a leading group in the construction of superconductor qubits. The team initially gained a lot of experience with a 9-qubit quantum computer and then decided to scale up the same technology to a much larger quantum computer.

In spring 2018, Martinis‘ group announced that a „supremacy-able“ quantum computer with the name “Bristlecone” was in test. Google stated the size of Bristlecone being staggering 72 qubits! At that time, the largest quantum computer was only 20 qubits in size.

At that time, nobody had thought such a huge leap in development was possible. You remember: A quantum computer doubles its potential with every additional qubit. At least in theory, Bristlecone would have 1,000 trillion times the performance of a 20 qubit device.

At this point, it already seemed as if the proof of quantum supremacy was imminent.

Google’s quantum computer “Sycamore”

After this announcement, however, it became quiet around Google’s ambitions. Google continued to expand its “stack” and published the programming interface “Cirq” for the remote control of quantum computers based on the computer language Python. In addition, the team around Neven and Martinis developed a number of interesting, scientific results on quantum hardware construction and quantum algorithms (some of which I refer to in other articles). Yet at first, in terms of quantum supremacy, there was nothing new.

A small impression of the hardware problems which Google’s team was probably struggling with during this period can be found in Alan Ho’s talk at the “Quantum For Business 2018” conference in December 2018 ^vii, in which the Google employee, among other things, called the other manufacturers for closer cooperation.

Perhaps due to this “dry spell” the team decided to downsize Bristlecone at some point. The new quantum computer got the name “Sycamore” and has a size of 53 fully functional qubits, which are arranged on a chip like a checkerboard. The quantum computer is cooled down almost to absolute zero temperature. Only at this point become the 53 non-linear oscillating circuits of the chip superconducting and “condense” into qubits with real quantum properties.

Martini’s group generate the “quantum gates”, the elementary operations of the quantum computer, using microwave radiation. Sycamore is able to execute the quantum gates on every single qubit via an external control electronics that works at room temperature. For the calibration of the individual quantum gates, Google’s team used the same test routines that were also used to demonstrate quantum supremacy (more on this below).

In order to be able to establish the couplings among the qubits, a quantum computer generally also requires a two-qubit quantum gate.

On a quantum computer usually certain gates with names “CNOT”, “CZ” or “iSWAP” are used for this. They change qubit B depending on the state in qubit A. The group led by John Martinis chose a different route: The researchers adapted new, quasi-mixed gates optimized to the real physics of Sycamore. Using a learning algorithm, they determined the corresponding degree of mixing for each individual 2-qubit coupling.

The computing task : “Random Quantum Circuit Sampling”

Already with their 9-qubit quantum computer, the group around John Martinis gained experience with a very special calculational task, which was a promising candidate for the proof of quantum supremacy ^viii.

The basic idea for the task is actually pretty obvious and goes back to Richard Feynman’s basic idea, which led to the development of quantum computers: Let’s assume that a conventional computer can no longer simulate or calculate a pure quantum system once it reaches a certain size. In particular, this would also mean that a conventional computer can no longer simulate certain quantum programs on a sufficiently large quantum computer. These quantum programs would only need to be sufficiently complex to ensure that the problem cannot be simplified or disassembled in any way to be computable on a conventional computer.

The easiest way to do this is to use completely random qubit operations on randomly selected qubits: A quantum program that is thrown together by pure chance. At the end of the random calculation, all qubits are measured and a series of zeros and ones, i.e. a series of bits, is the result of the calculation. By repeating the measurement several times for the same quantum program, a list of bit rows is obtained. At some point the list becomes so long that individual rows are being repeated certain times. The repetitions are random, but they are not evenly distributed! It is precisely this interference pattern of the different series that characterize the respective quantum program.

The process is called “Random Quantum Circuit Sampling”. The idea is as simple as brilliant. Of course, the implementation is a Herculean task (by the way, I’ll explain why this calculation is so difficult for conventional computers at the end of this article).

Sadly, at the end we only get rows of randomly selected zeros and ones. Unfortunately totally useless!

Or who would be interested in completely random bit strings?

At most, maybe the website www.random.org.

Wait a moment!

Why the heck is there a site like random.org?

A real application: quantum-certified random numbers

Kind of like that, the well-known computer scientist Scott Aaronson from the University of Texas, in his inimitable way, presented his protocol for “quantum-certified” random numbers in 2018. Aaronson surprised the experts with a talk on sampling random numbers ^ix. In it, he outlined his protocol, which is specially tailored to the first generation of supremacy-abled quantum computers.

It turns out that reliable random numbers are actually of value.

Of considerable value.

Random numbers are essential for many algorithms and for many areas in computer science: especially for cryptography. Last but not least, the NSA scandal made it obvious that compromised random numbers are a real problem for transmission security. Aaronson’s quantum-certified random numbers have the amazing property that they are proven to be true random numbers, even if the generating system is insecure and the publisher is not trustworthy.

The heart of Aaronson’s protocol is precisely the fact that the frequency with which a certain series of zeros and ones is present must obey a quantum distribution. This distribution, Aaronson argues, can no longer be simulated or manipulated once it reaches a certain row size. It can only be verified by a sufficiently large quantum computer. Then we know that the rows of bits originated straight from a quantum computer, and then they really have to be real random numbers. Then manipulation is impossible because a quantum computer always delivers real random numbers. You will see again below what I mean by the keyword “XEB routine”.

To get an impression which other areas of application might be slumbering in Sycamore, you can read my article „Anwendungen für Quantencomputer“.

The final: Google’s proof of quantum supremacy

But let’s finally get to the very heart of this article.

Google finally had a suitable quantum computer ready for operation that worked reliable enough to accomplish the actual task. The team had also determined a suitable calculation task. Now the scientists let Sycamore compete against the best current supercomputers.

First, the group around Martinis and Neven reduced the chessboard-like arrangement of the qubits to different, significantly smaller sections and let the quantum algorithm run. They further refined this simplification by allowing simple couplings between several cutouts on the qubit chessboard. They compared the list of bit strings they received with a quantum simulation on a simple, conventional computer that could still handle the reduced computing task.

To this end, the researchers compared the frequency with which a single bit pattern was measured in the quantum computer with the frequency with which the same bit pattern was measured using the simulation. They had previously developed a special test routine for this benchmark process (with the dazzling name “Cross Entropy Benchmark Fidelity”, or “XEB” for short). This XEB routine is designed in such a way that even the smallest deviations in frequency deliver large deviations in the benchmark result.

In fact, the benchmark results were consistent.

Then they gradually enlarged the cutouts on the qubit chessboard and repeated their comparison. The task quickly became too complex for normal computers. The team had to apply for computing time in Google’s enormous data centers ^x.

In addition, the team ran a complete 53-qubit simulation but with simplified quantum circuits and compared them again with the results on Sycamore.

The benchmark results again matched.

At some point, they must have included additional hardware: This is where the supercomputer at the Forschungszentrum Jülich in Germany comes into play, which they also mentioned in their article. In the end, they even included the largest current supercomputer: IBM’s “Summit” supercomputer at the Oak Ridge National Laboratory in the USA. They used various “state-of-the-art” simulation methods for quantum systems to simulate the quantum calculation.

In the end, a clear picture emerged.

The supercomputers were able to carry out the simulation up to certain cut-out sizes and came to the same benchmark results as Sycamore. They could no longer handle the calculational task for larger sections. The quantum calculations themselves had a complexity of up to 1113 one-qubit gates and 430 two-qubit gates (you can imagine that there is even more to be mentioned about these real circuits ^xi).

To perform such a quantum calculation on all qubits and to read out the qubits a million times with a million random 53-bit rows, Sycamore took 200 seconds. The major part was even spent on the control electronics. The calculation on the quantum chip actually only took 30 seconds.

For the simulations, on the other hand, Google’s team extrapolated the computing time of the simplified arithmetic to the entire 53-qubit chess board and came to the following conclusion:

The examined supercomputers would have required a runtime of 10,000 years for the full computing task!

“Quod erat demonstrandum”

(which was to be proved)

Now what about IBM’s objection?

After Google’s preliminary version of the work had been released to the public, various researchers had the opportunity to examine the article. IBM’s quantum computer research group did just that … very intensely:

In the best scientific manner, they developed a counter-argument that was supposed invalidate Google’s results at least partially. Of course, not entirely unselfish, because in terms of quantum computers, their group was way ahead until Google’s publication.

I just want to mention what Scott Aaronson, the one with the quantum-certified random numbers, had to say or to write about the subject. Not only had he been commissioned by the journal “Nature” to examine Google’s work, he is also a well-respected and interesting science blogger ^xii.

IBM has probably proven that Google’s quantum simulation was not optimal. Their improved simulation method would not have taken 10,000 years, but 2½ days, for the computing task using their “Summit” supercomputer in the Oak Ridge National Laboratory in the USA. Which is of course a huge leap! And you can imagine the moaning of Google’s team in their building in Santa Barbara, California when they realized they had overlooked this simulation alternative (in fact, John Martinis had explicitely mentioned the possibility of a better simulation in their paper).

However, one has to note the following:

The “Summit” is a supercomputer battleship XXL on an area the size of two basketball courts. IBM’s calculation, which the group has not yet carried out but extrapolated, would require Summit’s total 250 petabytes = 250 million gigabytes of hard disk space, the main argument of their improved process ^xiii, and would have a gigantic energy consumption.

In comparison, Google’s Sycamore is more of a “cabinet” (and only because of all those cooling units). And by the way, even with IBM’s simulation, Google’s quantum algorithm would be 1100 times faster (in time). If you compare the number of individual calculation steps (or FLOPS) instead of the time duration, Google would even be a factor of 40 billion times more efficient.

Also, even the IBM team does not deny that even their simulation would require an exponential effort for the task and Google’s quantum algorithm simply does not. This means that if Google were able to give Sycamore a few extra qubits, the true balance of power would quickly be apparent: with 60 qubits, IBM’s method would probably require 33 summits, with 70 qubits one would have to fill an entire city with summits, …

Aaronson compares this scientific competition with the chess games between the grand master Gary Kasparow and the computer “Deep Blue” (by the way, ironically made by the manufacturer IBM) in the late 1990s. The best established forces may be able to keep up for a while in the race, but soon they will be far behind.

Why no supercomputer can do this calculation

Incidentally, “Quantum Circuit Sampling” is also a wonderful example to illustrate the “quantum advantage” that a quantum computer has over conventional supercomputers for such calculations:

In the course of the calculation, the measurement probabilities of the individual 53-bit rows are either further amplified or suppressed. In the end, a characteristic frequency distribution emerges. How could a conventional computer solve such a task?

Let us imagine a very simple and naive computer program that stores each bit row together with its frequency in a table in the RAM memory. In each program step, the different table entries influence each other, sometimes more and sometimes less.

How many different 53-bit rows can there be? This question sounds harmless at first, but the number is actually astronomically high: About 10 million * one billion, a number with 16 zeros before the decimal point!

A conventional computer would need well over 100 million gigabytes RAM to store as many 53-bit rows together with their frequencies in memory variables … By the way, how much RAM does your computer have? 8 gigabytes, maybe 16 gigabytes? (not that bad!)

In each computational step, out of a total of 20 steps, Google’s program revises the measurement frequencies of each bit row. In extreme cases, these depend on the measurement frequencies of all bit rows from the previous program step. These are 1 billion * 1 billion * 1 billion * 100,000 dependencies, a number with 32 zeros before the decimal point! How many seconds would a conventional computer probably take to touch as many dependencies even just once? For comparison: a normal processor can perform a handful of billions of operations per second … and our universe is not even 1 billion * 1 billion seconds old.

A conventional computer is literally overwhelmed by that many possibilities and dependencies. A quantum computer in turn only needs these 53 qubits and the almost 1,500 individual qubit operations. Incredible.

At first glance, it is also clear that Google‘s and IBM‘s quantum simulations must have been much more sophisticated than our naive example program.

By the way: The strategy of exponential complexity is also pursued by other algorithms for quantum computers of the NISQ era: E.g. for quantum chemistry, for optimization problems or for quantum neural networks (there one speaks of „Variational Quantum Algorithms“). The “Random Quantum Circuit Sampling” is the candidate for which this has now been shown to be the first to achieve an exponential improvement.

A missed “moon landing moment” for Google’s team?

Without a doubt, the scientific bang was also planned as a media bang. In the meantime, Google was overtaken by the events, which is not surprising when you consider how many people were involved.

In the end, this should not detract us from the achievement of Google’s team: The group led by John Martinis and Hartmut Neven has probably written history by proving quantum supremacy.

Scott Aaronson wrote in his blog ^xiv:

„The world, it seems, is going to be denied its clean “moon landing” moment, wherein the Extended Church-Turing Thesis gets experimentally obliterated within the space of a press conference … Though the lightning may already be visible, the thunder belongs to the group at Google, at a time and place of its choosing.“

Footnotes