Author: Jens Marre

Quantum computers use the enigmatic quantum mechanics to provide completely new types of computing systems . That’s why quantum computer properties have an almost incredible effect: For example, the performance of a quantum computer increases ” exponentially”, so to speak explosive, with increasing size. In the following I will explain the special properties of a quantum computer in simple words and I will go into more detail about the amazing quantum programs .

The bang: the Shor algorithm

In 1994, mathematician Peter Shor from the renowned Massachusetts Institute of Technology / MIT had the idea of ​​his life. An idea that would herald a new era.

Shor investigated a new method to break down an integer into prime numbers. This prime factorization is an extremely complex matter. Even very powerful supercomputers take several years to break down very large numbers into prime numbers. ⁱ

This is one of the reasons why it is used for secure data encryption on the Internet. It is very easy to assemble even large numbers from known prime numbers (e.g. 7 × 13 × 13 × 17 × 53 = 1065883). Since the reverse is almost impossible, encryption on the Internet is bombproof.

Actually!

Shor wondered if the new method could be used to create new prime number algorithms. At some point he remembered a compulsory lecture on quantum mechanics, which he had had to listen to when he was a math student at the California Institute of Technology (Caltech). He had the terrific idea that the method could achieve the goal much faster if the calculation was not a conventional computer, but a quantum computer. He spent a year tinkering with his quantum algorithm and in the end actually came to the desired result ⁱⁱ.

Shor’s algorithm hit like a bomb. Up to this point, no one had been able to build a quantum computer. However, the Shor algorithm was the first proof of how immensely powerful a quantum computer would be and what social effects it would have. Shor’s algorithm triggered a veritable boom in the quantum computer scene.

A quantum computer takes advantage of the extraordinary properties of the atomic world to achieve completely new dimensions in computing speed using special quantum programs, the quantum algorithms. The word “extraordinary” is probably still understated . The quantum world is a puzzling world with almost magical properties.

To get an idea of ​​what is special about a quantum computer, we first have to look at how a conventional computer works.

Simply Explained: How does a conventional computer work?

Let us take the computer you are reading these lines with. It controls information in the form of zeros and ones via bits or bytes. The number “71” is represented, for example, by the bit series “0100 0111” and the letter “J”, by convention, by the bit series “100 1010”. Your computer remembers whether a row of bits represents a number, a letter, an image, or music. The bits themselves exist in the form of billions of electrical on / off switches, the transistors. Together they form the main memory of your computer. A good conventional computer has about 16 * 8 billion bits, or in other words: 16 gigabytes. A computer program manipulates these bits in individual arithmetic steps using the most elementary building blocks of human logic: AND operations, OR operations, NOT operations. These links are also called “gates” (English gates). A NOT link reverses a single bit, for example, to its opposite: NOT 0 = 1, NOT 1 = 0.

Using clever electrical circuits, the data bus, your computer is able to selectively control, read or overwrite each of the countless bits in the working memory with new values. A calculation step then looks like this, for example:

“Read out the value of the bit with the address number 1543216 and the value of the bit with the address number 6543 and combine the two values ​​with an AND command. Save the result in the bit with the address number 789874 “. By cleverly arranging these elementary AND, OR, NOT connections, one after the other, your computer can, for example, take two numbers together. After each of these calculation steps, your computer writes the intermediate results back into the main memory and calls them from there again for the next calculation step. The program for taking pictures looks unnecessarily complicated and mechanically stupid. However, since your computer is capable of executing billions of arithmetic steps per second, it is ultimately superior to every human being in such tasks.

The qubits simply explained

In contrast, a quantum computer does not control the information via simple on / off switches, i.e. the conventional bits, but via so-called “qubits” (for quantum bits). In a qubit, the values ​​0/1 or on / off are simultaneously available in a superimposed form. At first glance, this may look harmless. In fact, this overlay is one of the great mysteries of quantum mechanics.

As a consequence, the Austrian Nobel Prize winner Erwin Schrödinger invented his famous thought experiment “Schrödinger’s Cat” almost a hundred years ago: a cat that is overlaid with a qubit. The qubit turns on a poison cocktail as soon as it has the value 1. If the qubit has the value 0 and the value 1 at the same time, according to Schrödinger, the cat should also be dead and alive at the same time.

In my article “The Qubit and a Magician at Britain Has Got Talent” I compare the Qubit with a spectacular magic trick by the magician Darcy Oake in the 2014 English talent show. Darcy Oake appears to be on stage twice at the same time. A qubit behaves the same way. Not as a trick, however, but in reality.

To illustrate this, I use a qubit representation on “quantum-computer-explained.com”, which is simplified compared to the textbook representation but is very close to the core: a simple pointer in one level. For example, the following qubit is in equal parts both in state 0 and in state 1.

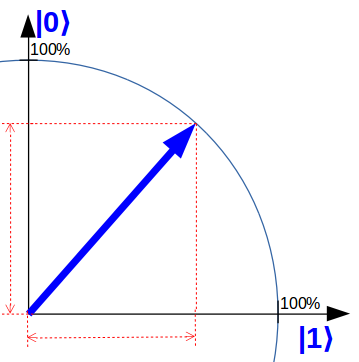
If you think now: “Got it! Then two qubits would simply be two pointers, ”I unfortunately have to disappoint you. The quantum computers don’t make it that easy for us. In fact, two qubits in the simplified representation still correspond to one pointer , but with four vertical axes !

I know that any attempt to somehow visualize four dimensions ends miserably. I want to try anyway:

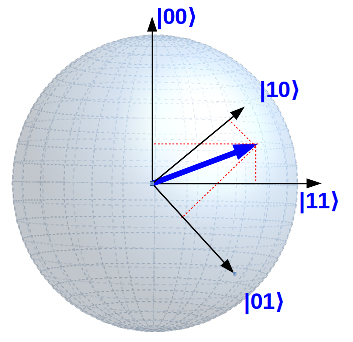
You can imagine that this behavior has very unusual consequences … More on this in the section on “Quantum Entanglement”.

The second such extraordinary feature of qubits is the following. Even the smallest amount of qubits in a quantum computer can simultaneously absorb and process a huge amount of information: ⁱⁱⁱ

• • • 1 qubit corresponds to 2 conventional bits
    • 2 qubits correspond to 4 conventional bits
    • 10 qubits correspond to 16 conventional kilo-bytes
    • 20 qubits correspond to 16 conventional megabytes
    • 30 qubits correspond to 16 conventional gigabytes
    • 31 qubits correspond to 32 conventional gigabytes

Each additional qubit doubles the number of information that can be used simultaneously! The performance of a quantum computer increases exponentially ! And this is how it goes on:

• • • 45 qubits correspond approximately to the memory size of the largest current, conventional supercomputer

• • • 50 qubits, the “quantum superiority” limit: The, at least theoretical, limit at which a quantum computer can perform certain calculations that would not be possible with any of the current supercomputers. ^iv The tech giants are battling it out at exactly this limit.
  • • 250 qubits: the absolute limit that would even be feasible for conventional computers. To achieve the memory size of a 250 qubit quantum computer, a conventional computer would have to use every atom in the universe as a conventional bit.

It sounds incredible. And it is!

And now consider that the quantum computer industry has the goal to build quantum computers with millions of qubits!

Quantum computers simply explained: quantum parallelism, superposition

The punch line with these enormous numbers is actually the following: let’s take the example with the take again. Your conventional computer takes two numbers , in the form of two rows of bits in the working memory, executes the specified program of individual arithmetic steps and finally receives one number in the form of a row of bits.

In contrast, a quantum computer takes two qubit rows for a task, saves the intermediate results again in qubits and finally receives the result in the form of a qubit row ^v. However, since a qubit series can contain huge amounts of information at the same time (see above), the quantum computer can ultimately execute the program simultaneously with a huge amount of numbers. This is the quantum parallelism. Usually, however, one speaks of “superposition”.

In fact, this form of overlay occurs more often in nature and not only in quantum mechanics ^vi. What makes quantum parallelism so special is the fact that only a few qubits can overlay such unimaginably large amounts of data. The qubits are not only superimposed individually, but the entire network of qubits. And it is precisely here that the number of possible combinations increases so rapidly. For three qubits, for example, up to eight possible bit states are used simultaneously (this corresponds to 2 ³ ): namely 000, 100, 001, 101, 011, 111, 010 and 110.

But: Every measurement destroys the quantum properties

Unfortunately, the enormous parallel computing power of a quantum computer has a big catch: it only works as long as the quantum computer is perfectly isolated from its surroundings and the highly fragile qubits are undisturbed. By reading the result of the quantum program from the qubits at the end, however, we are doing exactly that. At this moment, the values ​​that are present “decay” and only a single value remains, which is also chosen at random . This decay is known as the “collapse of the wave function” and is yet another mystery of the quantum world. It was the reason why some physicists, including Albert Einstein himself, appreciated and pushed quantum theory but basically rejected it: “God does not throw dice”.

Incidentally, such disturbances have almost insoluble consequences for the construction of quantum computers. How you can “protect” quantum properties against it, and what fundamental meaning this “quantum error correction” could have even for the nature of space and time, I will explain in the next Artikel „Der sehr, sehr steile Weg zum ersten Quantencomputer“.

And now? What is won if everything ultimately depends on pure chance?

Now comes the but: We can influence the probabilities with which the various values ​​are ultimately read out or measured. The art of a quantum program is, among other things, to manipulate the qubits in such a way that the result sought is most likely to be measured in the end. Until then, i.e. while he is still isolated from his surroundings, the enormous computing power of the undisturbed quantum computer can be used.

You can find out more about quantum programs below. Let us first come to one of the strangest properties of quanta or qubits.

Einstein’s spooky entanglement

I had already shown a pointer example for two qubits above. This pointer property has a bizarre consequence. In 1935, Albert Einstein personally predicted it in a famous essay: The “quantum entanglement” (English “entanglement”, he himself referred to the phenomenon as “spooky long-distance effect”). We can overlay two qubits (or several qubits) in such a way that we can no longer recognize them as individual qubits. Instead, they form a completely new, uniform state. They appear “entangled”: A measurement on the first qubit has an immediate effect on the second qubit.

To clarify this, let’s look again at a pointer diagram with 4 axes. The blue pointer below describes the common state of Qubit A and Qubit B. Now we only measure on Qubit B. In the previous section, you learned that qubit B decides on a state by measuring : We measure either state 0 or state 1 . We have not yet carried out a measurement on Qubit A. In fact, for Qubit A , we should have received a single, superimposed pointer in two dimensions that “knows ” nothing about the previous and independent measurement on Qubit B.

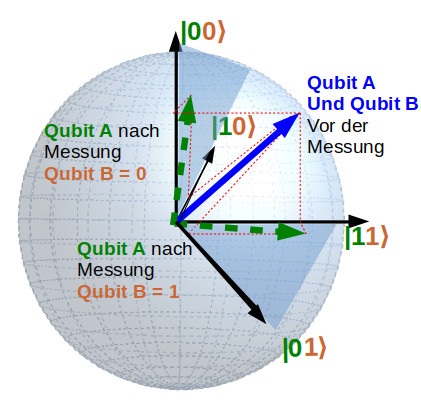
You can see from the example, however, that the measurement has a direct effect on Qubit A. After the measurement, Qubit A is something like the “shadow” of the original blue pointer , which I indicate with the dashed pointer. The level in which this shadow lies is determined by the measurement of Qubit B : If we measure the state 0 for Qubit B , we get for Qubit A the left dashed pointer, which mainly points in the 0 direction . If we have the state 1 for Qubit B, we get the lower dashed pointer for qubit A, which mainly points in the 1 direction .

The goal of Einstein’s work was actually to prove a fundamental mistake in quantum mechanics . According to Einstein, this entangled entity would have to remain, even if the two qubits were light years apart . That is why he spoke of long-range effects . The crazy thing is: all experiments suggest that it is the same. The long-distance effect is real in the quantum world and it has an immediate effect !

Such entangled forms of state do not exist anywhere else in the natural sciences . Maybe with one exception: a so-called astronomical “wormhole”, which can connect two black holes over a distance of many light years, as a kind of hyper-expressway. The question of how these two phenomena are related is actually the subject of current research in theoretical physics.

Quantum gates simply explained: The building blocks of quantum programs

We can’t just run the same algorithms that work on a conventional computer on a quantum computer. Instead, we have to construct completely new and strange quantum algorithms for quantum computers.

For this purpose, a quantum computer also uses elementary logic modules, the “quantum gates” (quantum gates) in every calculation step. However, these do not reflect our normal everyday logic, but rather quantum logic: The elementary building blocks are therefore no longer called AND, OR or NOT. Instead, a quantum computer uses logic modules that are called Hadamard, X, S, T, Z, Controlled NOT or Controlled Z, for example. The way these quantum gates function is less like the known building blocks of our everyday logic than they are rotations in a huge abstract “hyperspace” (or more precisely: a “Hilbert” space). In their entirety, the qubits form a single pointer in this space, which is rotated by each individual quantum gate. For two qubits, you had an impression of it earlier.

This fundamental strangeness compared to our everyday logic is the reason why a quantum program can only be deciphered and understood by connoisseurs of quantum algorithms.

For all representations of quantum gate circuits I use the excellent quantum computer simulator “Quirk” on “quantencomputer-info.de”:

http://algassert.com/quirk

Quirk is publicly available and can be tried directly in your browser (via “WebGL”). Craig Gidney, the Quirk programmer, modeled a number of well-known quantum algorithms. You should definitely take a look there. My favorite is the “quantum teleportation”, in which the author uses an animation to very nicely illustrate how a qubit state can be tele-transported to a second qubit by entangling it over a distance. By the way, Gidney is now employed by Google and has developed the quantum programming interface “Cirq” in the lead.

In every area of ​​conventional programming there is a lively IT scene on the Internet that has a strong influence on further development: be it servers, networks. Databases, Internet, programming, … The IT scene for quantum programming is still mainly located in the research facilities of universities and mainly in the special departments of Google, IBM, Microsoft & Co and some startups for quantum computers. Since spring 2018 there has been the new discussion forum “Quantum Computing Stack Exchange” ^vii , which is developing very lively and with high quality content. Important results will still be published on complicated scientific papers.

The most significant consequence of this publication was Peter Shor’s algorithm from 1994, which is able to crack the data encryption that was believed to be secure on the Internet. In the meantime, other, extremely fast and probably also more interesting quantum algorithms have been constructed.

Example from the Quirk homepage: Schematic structure of the Shor algorithm.

All providers of quantum computers have now developed programming interfaces. Via these interfaces, the quantum programs can be executed either by simulator on your own PC or from your own PC by remote control on the manufacturer’s cloud quantum computer. The following program excerpt shows Google’s example of the Shor algorithm in Google’s own programming interface “Cirq”.

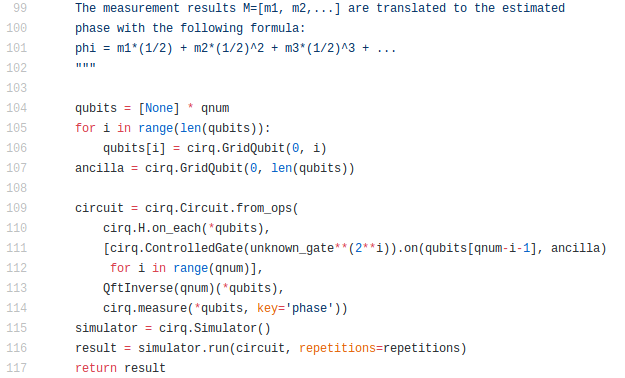
You can also see from these examples how much quantum programming is still in its infancy. All programs are currently still written in a kind of “machine code for quantum computers” and are therefore difficult to decipher. In the coming years and decades, quantum programming will also have to develop further in this regard. The software development for conventional digital computers showed us how. In the course of time, more and more intuitive programming languages ​​have emerged that abstract the actual machine code better and better.

Find the Ace of Spades! A quantum algorithm simply explained

To give you an impression of the different nature of the quantum algorithms, let’s try to solve the following problem:

Someone shuffles a card game with 52 cards well for us and spreads out the 52 cards indiscriminately and face down in front of us. Now he writes a number on each back of the card, the “address”. The task should be: Find the card, i.e. the address number, with the ace of spades!

With our everyday logic and for every conventional computer, the best algorithm for the solution is very simple and obvious:

• • • Step 1: take any card
    • Step 2: turn it over and check: is it the ace of spades?

• • • • • If so : You are done!
        • If not : You put the card aside and start again at step 1.

On average we need ½ * 52 = 26 runs for the solution. No single person and no single processor core could ever perform this task faster. Point!

The processor of a quantum computer can do this very well. For him, the solution looks completely different and bizarre. Because of the quantum parallelism, the quantum computer can view all cards at the same time and check them. He can, however, not easily fetch the card he is looking for, or more precisely the address number for this card. Instead, he has to gradually “hide” the wrong cards and gradually “show in” the ace of spades. In the end, only the ace of spades with the address number you are looking for remains.

The algorithm for this is the famous Grover algorithm. I introduce it in detail in my Artikel „Der Grover-Algorithmus und die Suche nach dem Heiligen Gral“You will also see how extremely important and profound this at first glance is banal question. The task could also be slightly modified: “Find the shortest route of all possible routes” or even “Find the proof for … (an important mathematical problem)”.

For our map example, the Grover algorithm works as follows:

In our quantum computer, we first assigned a bit pattern to each card. Ultimately, we are looking for the bit pattern for the ace of spades. Someone else has now “hidden” these bit patterns in the qubit registers of our quantum computer. We do not know where and instead we only get some address numbers for the respective registers. Of course, these address numbers are qubits again.

• • Step 1: First we convert the qubits of all address numbers into a uniformly superimposed quantum state.

• • Step 2: Then we reload the unknown bit patterns of the cards and “pin” them to their respective address numbers (this operation is also called “Quantum RAM”).

• • • • We now have a single state in which all cards including their address numbers are equally involved (the qubits of the addresses and the qubits of the bit patterns are maximally interwoven with each other).

• • • • You can “imagine” this state as a single pointer in a huge, abstract room with 52 dimensions or directional axes. But don’t try it at all. We can’t imagine more than three dimensions anyway: top / bottom, left / right, front / back.

• • • • Each of the 52 direction axes corresponds to a specific map. The Ace of Spades is one of these axes. Our superimposed state points completely obliquely into this room and a little in each of the 52 directions.

• • Step 3: The quantum computer now checks in which direction the ace of spades lies.

• • • • In principle, this test is a simple subroutine, it is nevertheless called something mysterious: the “oracle”. Figuratively speaking , the quantum computer uses the oracle to turn the pointer in the Ace of Spades direction.

• • • • Unfortunately, he can only turn it by a small angle. The more cards that need to be checked, the smaller this angle.

• • • • After the test, the pointer is no longer a uniform overlay. It now points a little more in the Ace of Spades direction than the directions of the other cards.

• • Step 4: We now have to perform step 3 several times in succession. The scientist Lov Grover demonstrated in 1996 that the pointer was turned in the direction of the ace of spades after √ 52 ≈ 7.2 tests . After 7 tests we measure the qubits and get the bit representation of the ace of spades and their address number.

The following example shows the Grover algorithm for two qubits.

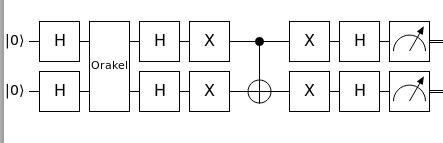
Quantum complexity simply explained

Half a century ago, computer scientists began dividing problems into classes depending on how difficult it was to find a solution. The problems that can be solved relatively effectively with a conventional computer are called P problems .

When the first concepts for quantum computers were developed, the problem class BQP was added. These are the problems that can be solved relatively effectively with a quantum computer.

It is now known that there is a fundamental difference between these two classes. In principle, a quantum computer is able to effectively solve much more problems than a conventional computer. An example of this is the division into prime numbers using the Shor algorithm.

The following diagram shows that even a quantum computer has its limits. It shows the relationship between the important problem classes that most computer scientists currently suspect (you can find out more about the classes shown in my article on the Grover algorithm):

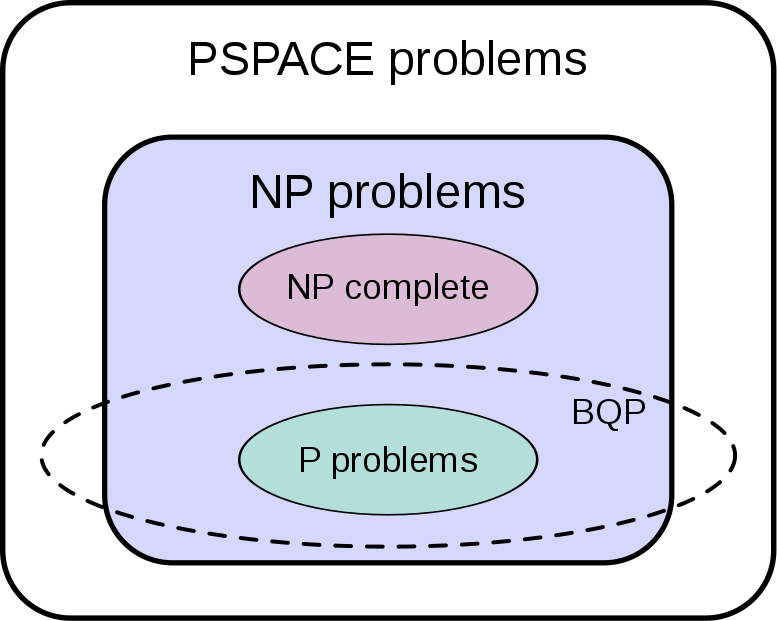
(Source: https://en.wikipedia.org/wiki/File:BQP_complexity_class_diagram.svg)

Footnotes

Google has recently demonstrated the so-called “quantum supremacy”. Quantum supremacy is the major milestone in the development of current quantum computers. Quantum supremacy marks the point in computer history at which a quantum computer has been proven to outperform all conventional supercomputers for a specific problem for the first time. I explain all the details, the exciting backgrounds and give you detailed explanations of this probably groundbreaking event.

A magic moment of science and technology

Science usually means struggling for knowledge in painstaking detail work, putting away failures, rethinking and moving on. Science also means celebrating small successes every now and then, together with a small crowd of like-minded colleagues. Successes that have brought the big picture a yet another little bit forward, usually unnoticed by the masses.

And then there are the very rare, the really big moments: the magic moments of science and technology. The last major building block in a long chain of previous events that is so powerful that it forces an entire new branch of knowledge into the public eye.

The Internet company Google recently managed to make a bang:

The tech giant’s “AI Quantum” team recently demonstrated “quantum supremacy” .

Google’s proof of quantum supremacy: A rumor is confirmed

The first tangible signs of this were already published in June. The online magazine Quantamagazine reported on an ominous calculation for which the tech giant’s enormous computing resources had to be tapped. In July, the Forschungszentrum Jülich in Germany issued a press release on a new partnership with Google ⁱ. Later it turned out that the Jülich supercomputer also played a certain role in Google‘s results.

At the end of September, NASA, one of Google’s partners in the matter, made a confidential preliminary version of Google’s research work available for download. Yet this was probably for internal purposes only, for a short time and in a well-hidden area on the website. However, not hidden enough for Google’s own search engine: The automated Google “crawler” became aware of the document shortly after publication and distributed it by hand.

The news spread quickly and several news sites reported about it.

Finally, Google reacted and made the document called “Quantum Supremacy Using a Programmable Superconducting Processor” available for download themself (together with an additional article) ⁱⁱ. For the time being, however, completely uncommented, as the work was in the “peer review” stage at this point.

I emphasize that Google did not announce its groundbreaking results prematurely, but waited for the proper scientific review process.

Yesterday, the official publication was published in the journal “Nature” ⁱⁱⁱ.

At the center of the work is the previously unknown quantum computer “Sycamore” from Google and a calculation that would probably take 10,000 years on the currently fastest supercomputers: Sycamore only needed 200 seconds.

At the beginning of this week, the IBM group for quantum computers put some more spice into the current developments with an additional interesting detail: With its improved simulation process, the fastest supercomputer would probably only have taken 2½ days.

In the following you will find all the details and the exciting background to this, probably nevertheless, groundbreaking event.

The development of the first quantum computer

Deep down, nature does not function according to our everyday laws, but according to the mysterious laws of the quantum world. For this reason, conventional computers quickly reach their limits when it comes to calculating natural processes on an atomic scale. Over 30 years ago, the legendary physicist Richard Feynman left the world of science with a visionary but almost hopeless legacy: only if we were able to construct computers based on this quantum logic, we could ultimately simulate and fundamentally calculate nature.

Once this idea was born, the topic quickly took off. The first huge bang came in 1994 when mathematician Peter Shor demonstrated that the encryption on the Internet, which has been believed to be bomb-proof, could be cracked in a matter of seconds with a very large quantum computer (not that a false impression arises: Shor’s algorithm plays no role in Google’s proof of quantum supremacy).

Yet, the technical hurdles for the actual development were and still are enormous. It took almost 20 years before the first very experimental minimal quantum computer was built in a research facility.

The NISQ era of quantum computers

Over time, the tech giants IBM, Google, Microsoft and Co recognized the huge potential of the new technology. They started collaborations with research groups, recruited top-class scientists and got involved in the development of quantum computers.

As a result, the first quantum computers, offered by tech companies, are now available in the cloud. Available to everyone. I describe the current status in my article “Which quantum computers already exist?”

Current quantum computers still have a very small size of up to 20 “qubits”, the quantum bits. Just like conventional bits, qubits can be in the states 0 or 1. In addition, they can also be in “superposed” states of both 0 and 1.

To illustrate this, for “quantum-computer-explained” I use a qubit representation, which is simplified compared to the textbook representation, but gets already quite close to the core: A simple pointer in a flat plain. For example, the following qubit is in equal parts both in the state 0 and in the state 1.

During a quantum calculation, the qubits get “rotated” in the plain and are measured at the end. By this measurement, the qubits “choose” a single state to end up at: 0 or 1. This decision is made purely by chance and is subject to the laws of quantum mechanics. The more the qubit pointed in the direction of a state before the measurement, the more likely this state is being measured afterwards.

The real highlight is the following: A quantum computer doubles its potential computing power with each additional qubit: That is, exponentially!

You will find more about the fundamental differences between a conventional computer and a quantum computer in my introductory article “The incredible quantum computer simply explained” .

The current quantum computers are still in the so-called “NISQ era”. This stands for “Noisy Intermediate Scale Quantum”, i.e. error-prone quantum computers with a “moderate” size of a few hundred “qubits”, in perspective.

What is quantum supremacy?

To give you an impression of it: The Shor algorithm would probably require hundreds of thousands of qubits and millions of arithmetic operations.

The quantum computer community is therefore driven by a big question:

Can you already do a calculation on a quantum computer,

1. 1. 1. that has a real practical use and
      2. that no conventional supercomputer could ever do?

Over the years, several practical quantum algorithms have actually been developed that can even run on current quantum computers. The problem is, that these calculations could be carried out easily even with a normal laptop.

By now it has become obvious that the search for such an algorithm is currently a too great task.

For this reason, the community has focused on point no. 2 for the past years: Is a current quantum computer able to outperform even the largest supercomputer for a single calculation, regardless of whether it has any practical use or not?

And this is exactly what quantum supremacy is all about.

John Preskill from the California Institute of Technology (Caltech), one of the leading scientists in quantum computer research, had calculated the sound barrier of quantum supremacy in 2012 ^iv. By this he has also given the go-ahead for a technological race. With a size of 49 or 50 qubits, a quantum computer should be able to perform certain calculations much faster than any conventional supercomputer. A quantum computer with this size should be able to show off its inherent and deeply built in speed advantage.

What is the significance of Google’s proof of quantum supremacy?

So to prove quantum supremacy, you only need a single calculation.

On the one hand, this claim sounds a bit ridiculous. As to say “Let‘s make it as simple as possible so we will succeed for sure”. Real “supremacy” should look different: For every other computing task, conventional computers are still miles ahead of current quantum computers.

On the other hand, the project also sounds absolutely absurd: Even a normal laptop works with billions of conventional bits and several processor cores. A supercomputer in turn operates in spheres that are several orders of magnitude higher. For many decades, computer science and IT have been working to make computer programs even better, faster. We can admire the success of these developments all around us in our digitized world.

It is therefore completely absurd to assume that we could construct any new type of programmable, universal computing machine, with just a few dozen “whatever bits” that could compute just a single task fundamentally better than the very best of our celebrated computers.

Ultimately, this is just what an “ancient” hypothesis from the early days of theoretical computer science deals with: The “Extended Church Turing Thesis”. It says just the opposite: Any type of universal computing machine can be efficiently mimicked or simulated by a conventional computer, and the opposite direction is just as true ^v. Or to put it more simply: We can continue to improve our computing techniques and the technology in our computers, but we can not fundamentally improve the very nature of our computing machines.

Anyone who demonstrates quantum supremacy has disproved the famous extended Church Turing thesis!

This is a fact.

Let‘s also get back to this „great moment“-thing: The miracle of such moments was often enough the prove of what is generally feasible.

Take the Wright brothers’ maiden flight, for example: On December 17, 1903, Orville Wright flew the first flight of a navigable propeller machine: 12 seconds long and 37 meters far. Thus, very manageable and actually not worth mentioning. Nevertheless, this moment has entered the history books ^vi. By the end of 1905 the brothers had been flying for almost 40 minutes and 40 kilometers.

We have to wait and see how the quantum computers will do …

Google’s way of proving the quantum supremacy

To demonstrate quantum supremacy, Google’s team had to master five extremely difficult tasks:

1. 1. 1. They had to design a universal quantum computer with about 50 qubits that was reliably able to correctly execute any quantum program.
      2. They had to find a calculation that was specially designed for this quantum computer and that actually uses all of its qubits and all standard operations for quantum computers (any other task could probably be efficiently accomplished by conventional computers).
      3. They had to do this calculation on the quantum computer.
      4. They had to demonstrate that the final result of the calculation is most likely correct.
      5. They had to demonstrate that no conventional computer can perform this computing task in a timely manner, not even the fastest supercomputers.

Of all these tasks, the first task was certainly the most difficult one.

Google’s team forms

Google has gained experience in the field of quantum computers for several years and in 2013 founded the “AI Quantum” team, led by the German IT specialist and long-time Google employee Hartmut Neven. Previously, Neven was a leader in the Google Glass project.

In 2014, Neven’s team started a collaboration with the well-known physicist John Martinis from the University of California, Santa Barbara. He was to lead the construction of a new quantum computer. Martinis team is a leading group in the construction of superconductor qubits. The team initially gained a lot of experience with a 9-qubit quantum computer and then decided to scale up the same technology to a much larger quantum computer.

In spring 2018, Martinis‘ group announced that a „supremacy-able“ quantum computer with the name “Bristlecone” was in test. Google stated the size of Bristlecone being staggering 72 qubits! At that time, the largest quantum computer was only 20 qubits in size.

At that time, nobody had thought such a huge leap in development was possible. You remember: A quantum computer doubles its potential with every additional qubit. At least in theory, Bristlecone would have 1,000 trillion times the performance of a 20 qubit device.

At this point, it already seemed as if the proof of quantum supremacy was imminent.

Google’s quantum computer “Sycamore”

After this announcement, however, it became quiet around Google’s ambitions. Google continued to expand its “stack” and published the programming interface “Cirq” for the remote control of quantum computers based on the computer language Python. In addition, the team around Neven and Martinis developed a number of interesting, scientific results on quantum hardware construction and quantum algorithms (some of which I refer to in other articles). Yet at first, in terms of quantum supremacy, there was nothing new.

A small impression of the hardware problems which Google’s team was probably struggling with during this period can be found in Alan Ho’s talk at the “Quantum For Business 2018” conference in December 2018 ^vii, in which the Google employee, among other things, called the other manufacturers for closer cooperation.

Perhaps due to this “dry spell” the team decided to downsize Bristlecone at some point. The new quantum computer got the name “Sycamore” and has a size of 53 fully functional qubits, which are arranged on a chip like a checkerboard. The quantum computer is cooled down almost to absolute zero temperature. Only at this point become the 53 non-linear oscillating circuits of the chip superconducting and “condense” into qubits with real quantum properties.

Martini’s group generate the “quantum gates”, the elementary operations of the quantum computer, using microwave radiation. Sycamore is able to execute the quantum gates on every single qubit via an external control electronics that works at room temperature. For the calibration of the individual quantum gates, Google’s team used the same test routines that were also used to demonstrate quantum supremacy (more on this below).

In order to be able to establish the couplings among the qubits, a quantum computer generally also requires a two-qubit quantum gate.

On a quantum computer usually certain gates with names “CNOT”, “CZ” or “iSWAP” are used for this. They change qubit B depending on the state in qubit A. The group led by John Martinis chose a different route: The researchers adapted new, quasi-mixed gates optimized to the real physics of Sycamore. Using a learning algorithm, they determined the corresponding degree of mixing for each individual 2-qubit coupling.

The computing task : “Random Quantum Circuit Sampling”

Already with their 9-qubit quantum computer, the group around John Martinis gained experience with a very special calculational task, which was a promising candidate for the proof of quantum supremacy ^viii.

The basic idea for the task is actually pretty obvious and goes back to Richard Feynman’s basic idea, which led to the development of quantum computers: Let’s assume that a conventional computer can no longer simulate or calculate a pure quantum system once it reaches a certain size. In particular, this would also mean that a conventional computer can no longer simulate certain quantum programs on a sufficiently large quantum computer. These quantum programs would only need to be sufficiently complex to ensure that the problem cannot be simplified or disassembled in any way to be computable on a conventional computer.

The easiest way to do this is to use completely random qubit operations on randomly selected qubits: A quantum program that is thrown together by pure chance. At the end of the random calculation, all qubits are measured and a series of zeros and ones, i.e. a series of bits, is the result of the calculation. By repeating the measurement several times for the same quantum program, a list of bit rows is obtained. At some point the list becomes so long that individual rows are being repeated certain times. The repetitions are random, but they are not evenly distributed! It is precisely this interference pattern of the different series that characterize the respective quantum program.

The process is called “Random Quantum Circuit Sampling”. The idea is as simple as brilliant. Of course, the implementation is a Herculean task (by the way, I’ll explain why this calculation is so difficult for conventional computers at the end of this article).

Sadly, at the end we only get rows of randomly selected zeros and ones. Unfortunately totally useless!

Or who would be interested in completely random bit strings?

At most, maybe the website www.random.org.

Wait a moment!

Why the heck is there a site like random.org?

A real application: quantum-certified random numbers

Kind of like that, the well-known computer scientist Scott Aaronson from the University of Texas, in his inimitable way, presented his protocol for “quantum-certified” random numbers in 2018. Aaronson surprised the experts with a talk on sampling random numbers ^ix. In it, he outlined his protocol, which is specially tailored to the first generation of supremacy-abled quantum computers.

It turns out that reliable random numbers are actually of value.

Of considerable value.

Random numbers are essential for many algorithms and for many areas in computer science: especially for cryptography. Last but not least, the NSA scandal made it obvious that compromised random numbers are a real problem for transmission security. Aaronson’s quantum-certified random numbers have the amazing property that they are proven to be true random numbers, even if the generating system is insecure and the publisher is not trustworthy.

The heart of Aaronson’s protocol is precisely the fact that the frequency with which a certain series of zeros and ones is present must obey a quantum distribution. This distribution, Aaronson argues, can no longer be simulated or manipulated once it reaches a certain row size. It can only be verified by a sufficiently large quantum computer. Then we know that the rows of bits originated straight from a quantum computer, and then they really have to be real random numbers. Then manipulation is impossible because a quantum computer always delivers real random numbers. You will see again below what I mean by the keyword “XEB routine”.

To get an impression which other areas of application might be slumbering in Sycamore, you can read my article „Anwendungen für Quantencomputer“.

The final: Google’s proof of quantum supremacy

But let’s finally get to the very heart of this article.

Google finally had a suitable quantum computer ready for operation that worked reliable enough to accomplish the actual task. The team had also determined a suitable calculation task. Now the scientists let Sycamore compete against the best current supercomputers.

First, the group around Martinis and Neven reduced the chessboard-like arrangement of the qubits to different, significantly smaller sections and let the quantum algorithm run. They further refined this simplification by allowing simple couplings between several cutouts on the qubit chessboard. They compared the list of bit strings they received with a quantum simulation on a simple, conventional computer that could still handle the reduced computing task.

To this end, the researchers compared the frequency with which a single bit pattern was measured in the quantum computer with the frequency with which the same bit pattern was measured using the simulation. They had previously developed a special test routine for this benchmark process (with the dazzling name “Cross Entropy Benchmark Fidelity”, or “XEB” for short). This XEB routine is designed in such a way that even the smallest deviations in frequency deliver large deviations in the benchmark result.

In fact, the benchmark results were consistent.

Then they gradually enlarged the cutouts on the qubit chessboard and repeated their comparison. The task quickly became too complex for normal computers. The team had to apply for computing time in Google’s enormous data centers ^x.

In addition, the team ran a complete 53-qubit simulation but with simplified quantum circuits and compared them again with the results on Sycamore.

The benchmark results again matched.

At some point, they must have included additional hardware: This is where the supercomputer at the Forschungszentrum Jülich in Germany comes into play, which they also mentioned in their article. In the end, they even included the largest current supercomputer: IBM’s “Summit” supercomputer at the Oak Ridge National Laboratory in the USA. They used various “state-of-the-art” simulation methods for quantum systems to simulate the quantum calculation.

In the end, a clear picture emerged.

The supercomputers were able to carry out the simulation up to certain cut-out sizes and came to the same benchmark results as Sycamore. They could no longer handle the calculational task for larger sections. The quantum calculations themselves had a complexity of up to 1113 one-qubit gates and 430 two-qubit gates (you can imagine that there is even more to be mentioned about these real circuits ^xi).

To perform such a quantum calculation on all qubits and to read out the qubits a million times with a million random 53-bit rows, Sycamore took 200 seconds. The major part was even spent on the control electronics. The calculation on the quantum chip actually only took 30 seconds.

For the simulations, on the other hand, Google’s team extrapolated the computing time of the simplified arithmetic to the entire 53-qubit chess board and came to the following conclusion:

The examined supercomputers would have required a runtime of 10,000 years for the full computing task!

“Quod erat demonstrandum”

(which was to be proved)

Now what about IBM’s objection?

After Google’s preliminary version of the work had been released to the public, various researchers had the opportunity to examine the article. IBM’s quantum computer research group did just that … very intensely:

In the best scientific manner, they developed a counter-argument that was supposed invalidate Google’s results at least partially. Of course, not entirely unselfish, because in terms of quantum computers, their group was way ahead until Google’s publication.

I just want to mention what Scott Aaronson, the one with the quantum-certified random numbers, had to say or to write about the subject. Not only had he been commissioned by the journal “Nature” to examine Google’s work, he is also a well-respected and interesting science blogger ^xii.

IBM has probably proven that Google’s quantum simulation was not optimal. Their improved simulation method would not have taken 10,000 years, but 2½ days, for the computing task using their “Summit” supercomputer in the Oak Ridge National Laboratory in the USA. Which is of course a huge leap! And you can imagine the moaning of Google’s team in their building in Santa Barbara, California when they realized they had overlooked this simulation alternative (in fact, John Martinis had explicitely mentioned the possibility of a better simulation in their paper).

However, one has to note the following:

The “Summit” is a supercomputer battleship XXL on an area the size of two basketball courts. IBM’s calculation, which the group has not yet carried out but extrapolated, would require Summit’s total 250 petabytes = 250 million gigabytes of hard disk space, the main argument of their improved process ^xiii, and would have a gigantic energy consumption.

In comparison, Google’s Sycamore is more of a “cabinet” (and only because of all those cooling units). And by the way, even with IBM’s simulation, Google’s quantum algorithm would be 1100 times faster (in time). If you compare the number of individual calculation steps (or FLOPS) instead of the time duration, Google would even be a factor of 40 billion times more efficient.

Also, even the IBM team does not deny that even their simulation would require an exponential effort for the task and Google’s quantum algorithm simply does not. This means that if Google were able to give Sycamore a few extra qubits, the true balance of power would quickly be apparent: with 60 qubits, IBM’s method would probably require 33 summits, with 70 qubits one would have to fill an entire city with summits, …

Aaronson compares this scientific competition with the chess games between the grand master Gary Kasparow and the computer “Deep Blue” (by the way, ironically made by the manufacturer IBM) in the late 1990s. The best established forces may be able to keep up for a while in the race, but soon they will be far behind.

Why no supercomputer can do this calculation

Incidentally, “Quantum Circuit Sampling” is also a wonderful example to illustrate the “quantum advantage” that a quantum computer has over conventional supercomputers for such calculations:

In the course of the calculation, the measurement probabilities of the individual 53-bit rows are either further amplified or suppressed. In the end, a characteristic frequency distribution emerges. How could a conventional computer solve such a task?

Let us imagine a very simple and naive computer program that stores each bit row together with its frequency in a table in the RAM memory. In each program step, the different table entries influence each other, sometimes more and sometimes less.

How many different 53-bit rows can there be? This question sounds harmless at first, but the number is actually astronomically high: About 10 million * one billion, a number with 16 zeros before the decimal point!

A conventional computer would need well over 100 million gigabytes RAM to store as many 53-bit rows together with their frequencies in memory variables … By the way, how much RAM does your computer have? 8 gigabytes, maybe 16 gigabytes? (not that bad!)

In each computational step, out of a total of 20 steps, Google’s program revises the measurement frequencies of each bit row. In extreme cases, these depend on the measurement frequencies of all bit rows from the previous program step. These are 1 billion * 1 billion * 1 billion * 100,000 dependencies, a number with 32 zeros before the decimal point! How many seconds would a conventional computer probably take to touch as many dependencies even just once? For comparison: a normal processor can perform a handful of billions of operations per second … and our universe is not even 1 billion * 1 billion seconds old.

A conventional computer is literally overwhelmed by that many possibilities and dependencies. A quantum computer in turn only needs these 53 qubits and the almost 1,500 individual qubit operations. Incredible.

At first glance, it is also clear that Google‘s and IBM‘s quantum simulations must have been much more sophisticated than our naive example program.

By the way: The strategy of exponential complexity is also pursued by other algorithms for quantum computers of the NISQ era: E.g. for quantum chemistry, for optimization problems or for quantum neural networks (there one speaks of „Variational Quantum Algorithms“). The “Random Quantum Circuit Sampling” is the candidate for which this has now been shown to be the first to achieve an exponential improvement.

A missed “moon landing moment” for Google’s team?

Without a doubt, the scientific bang was also planned as a media bang. In the meantime, Google was overtaken by the events, which is not surprising when you consider how many people were involved.

In the end, this should not detract us from the achievement of Google’s team: The group led by John Martinis and Hartmut Neven has probably written history by proving quantum supremacy.

Scott Aaronson wrote in his blog ^xiv:

„The world, it seems, is going to be denied its clean “moon landing” moment, wherein the Extended Church-Turing Thesis gets experimentally obliterated within the space of a press conference … Though the lightning may already be visible, the thunder belongs to the group at Google, at a time and place of its choosing.“

Footnotes